The Museum Of All Shells

This article is extracted from Chapter 6 of Climbing Mount Improbable, by Richard Dawkins. You can purchase and read the entire book here: Climbing Mount Improbable

Natural Selection is the pressure that drives evolution up the slopes of Mount Improbable. Pressure really is rather a good metaphor. We speak of ‘selection pressure’, and you can almost feel it pushing a species to evolve, shoving it up the gradients of the mountain. Predators, we say, provided the selection pressure that drove antelopes to evolve their fast running legs. Even as we speak, though, we remember what this really means: genes for short legs are more likely to end up in predators’ bellies and therefore the world becomes less full of them. ‘Pressure’ from choosy females drove the evolution of male pheasants’ sumptuous feathers. What this means is that a gene for a beautiful feather is especially likely to find itself riding a sperm into a female's body. But we think of it as a ‘pressure’ driving males towards greater beauty. No doubt predators provided a selection pressure in the opposite direction, towards duller plumage, since bright males would presumably attract predator, as well as female, eyes. Without the pressure from predators the cocks would be even brighter and more extravagant under pressure from females. Selection pressures, then, can push in opposite directions, or in the same direction or even (mathematicians can find ways of visualizing this) at any other ‘angle’ relative to one another, Selection pressures, moreover, can be ‘strong’ or ‘weak’, and the ordinary language meanings of these words fit well. The particular path up Mount Improbable that a lineage takes will be influenced by lots of different selection pressures, pushing and tugging in different directions and with different strengths, sometimes cooperating with each other, sometimes opposing.

But pressure isn't the end of the story. The path chosen up Mount Improbable will depend, too, on the shapes of the slopes. There are selection pressures, pushing and tugging in an assortment of directions and strengths, but there are also lines of least resistance and insurmountable precipices. A selection pressure may push for all it’s worth in a particular direction, but if that direction is blocked by an impassable cliff it will come to nothing. Natural selection has to have alternatives to choose among. Selection pressures, however strong, cant do anything without genetic variation. To say that predators provide a selection pressure in favour of fast-running antelopes is just to say that predators eat the slowest antelopes. But if there is nothing to choose between the genes of fast and slow antelopes—that is, if differences in running speed are purely environmentally determined—no evolutionary business will result. In the direction of improved speed, Mount Improbable might present no slope to climb.

Now we come to a piece of genuine uncertainty and a spectrum of opinion among biologists. At one extreme are those who feel that we can take genetic variation more or less for granted. If the selection pressure exists, they feel, there will always be enough genetic variation to accommodate it. The trajectory of a lineage in evolutionary space will be, in practice, determined by the tussle among selection pressures alone. At the other extreme are those who feel that available genetic variation is the important consideration determining the direction of evolution. Some even go so far as to assign natural selection a minor, subsidiary role. To take our two biologists to the point of caricature, we might imagine them disagreeing on why pigs dont have wings. The extreme selectionist says that pigs don’t have wings because it would not be an advantage for them to have wings. The extreme anti-selectionist says that pigs might benefit from having wings, but they can’t have them because there never were mutant wing stubs for natural selection to work upon.

The controversy is more sophisticated than that, and Mount Improbable, even in its multiple-peaked version, isn't a powerful enough metaphor to explore it. We need a new metaphor, using the kind of imagination that mathematicians enjoy although we shan't use explicit mathematical symbols. It will make more demands on us than Mount Improbable, but it is worth it. In The Blind Watchmaker 1 made brief excursions into what I variously called ‘genetic space’, ‘biomorph land’ and ‘Making Tracks Through Animal Space’, More recently the philosopher Daniel Dennett has penetrated further into this undiscovered country which, by poetic allusion to Borges’s Library of Babel, he calls the Library of Mendel. My version in this chapter is a gigantic museum of the zoological imagination.

Imagine a museum with galleries stretching towards the horizon in every direction, and as far as the eye can see upwards and downwards as well. Preserved in the museum is every kind of animal form that has ever existed, and every kind that could be imagined. Each animal is housed next door to those that it most resembles. Each dimension in the museum—that is, each direction along which a gallery extends— corresponds to one dimension in which the animals vary. For example, as you walk north along a particular gallery you notice a progressive lengthening of the horns of the specimens in the cabinets. Turn round and walk south and the horns shorten. Turn and walk east and the horns stay the same but something else changes, say the teeth get sharper. Walk west and the teeth grow blunter. Since horn length and tooth sharpness are only two out of thousands of ways in which animals can vary, the galleries must criss-cross one another in many-dimensional space, not just the ordinary three-dimensional space that we, with our limited minds, are capable of visualizing. This is what I meant when I said that we had to learn to think like a mathematician.

What would it mean to think in four dimensions? Suppose we are dealing with antelopes and we measure four variables: horn length, tooth sharpness, intestine length and coat hairiness. If we ignore one of the dimensions, say coat hairiness, we could place each of our antelopes in its rightful place in a three-dimensional graph—a cube—of the remaining variables, horn length, tooth sharpness and intestine length. Now how do we bring in the fourth dimension, coat hairiness? We do the whole cube exercise separately for all short-haired antelopes, then we produce another cube for all slightly longer-haired antelopes and so on. A given antelope will be placed, first in whichever cube pertains to its hair length and then, within that cube, to its rightful position determined by its horns, teeth and intestines. Coat hairiness is the fourth dimension. In principle you can go on constructing families of cubes, and cubes of cubes, and cubes of cubes of cubes until you have placed animals in the equivalent of many-dimensional space.

To get some idea of what we are supposed to be thinking of when we think of the Museum of All Possible Animals, this chapter will deal with a particular case which can, more or less, be confined to three dimensions. In the next chapter I shall return to the controversy with which this chapter began and try to make a constructive overture towards the other side (for I am a known partisan). This chapter's three-dimensional special case is that of snail shells and other coiled shells. The reason the galleries of shells can be confined to three dimensions is that most of the important variation among shells can be expressed as change in only three numbers. In what follows, I shall be following in the footsteps of David Raup, a distinguished palaeontologist from the University of Chicago. Raup, in turn, was inspired by the celebrated D’Arcy Wentworth Thompson, of the ancient and distinguished Scottish University of St Andrews, whose book, On Growth and Form (first published in 1919), has been a persistent, if not quite mainstream, influence on zoologists for most of the twentieth century. It is one of the minor tragedies of biology that D’Arcy Thompson died just before the computer age, for almost evety page of his great book cries out for a computer. Raup wrote a program to generate shell form, and I have written a similar program to illustrate this chapter although—as might be expected—lI incorporated it in a Blind Watchmaker-style artificial selection program.

The shells of snails and other molluscs, and also the shells of creatures called brachiopods which have no connection with molluscs but superficially resemble them, all grow in the same kind of way, which is different from the way we grow. We start small and grow all over (with some bits growing faster than others). You can't take a man and dissect out the bit of him that was him as a baby. With a mollusc shell you can do just that. A mollusc shell starts small and grows at the

margins, so the innermost part of the adult coil is the baby shell. Each animal carties its own infant form around with it, as the narrowest part of its shell. The shell of Nautilus (already mentioned for its pinhole eye) is divided into air-filled flotation compartments, all except for the largest and most recently built compartment at the growing margin, in which the animal itself lives at any one time (Figure 6.1).

Because of their method of expanding at the margin, shells all have the same general form. It is a solid version of the so-called logarithmic or equiangular spiral. The logarithmic spiral is different from the Archimedean spiral which is what a sailor produces when he coils a rope on the deck. No matter how many turns the rope takes, each successive turn is still the same width—one thickness of the rope. In a logarithmic spiral, by contrast, the spiral opens out as it propels itself away from the centre. Different spirals open out at different rates, but it is always a particular rate for any particular spiral. Figure 6.2 shows, in addition to an Archimedean coiled-rope spiral, two logarithmic spirals with different rates of opening out.

A shell grows, not as a line, but as a tube. The tube doesnt have to be citcular in cross-section like a French horn but, just for the moment, we'll assume that it is. We'll also assume that the spiral drawn represents the outer margin of the tube. The diameter of the tube could happen to expand at just the right rate to keep the inner margin fitting snugly against the previous whorl of the spiral, as in Figure 6.3a. But it doesn't have to. If the tube’s diameter expands more slowly than the outer margin of the spiral, a gap of increasing size will be left between successive whorls, as in Figure 6.3b. The more ‘gappy’ the shell, the more it seems suitable for a worm rather than for a snail.

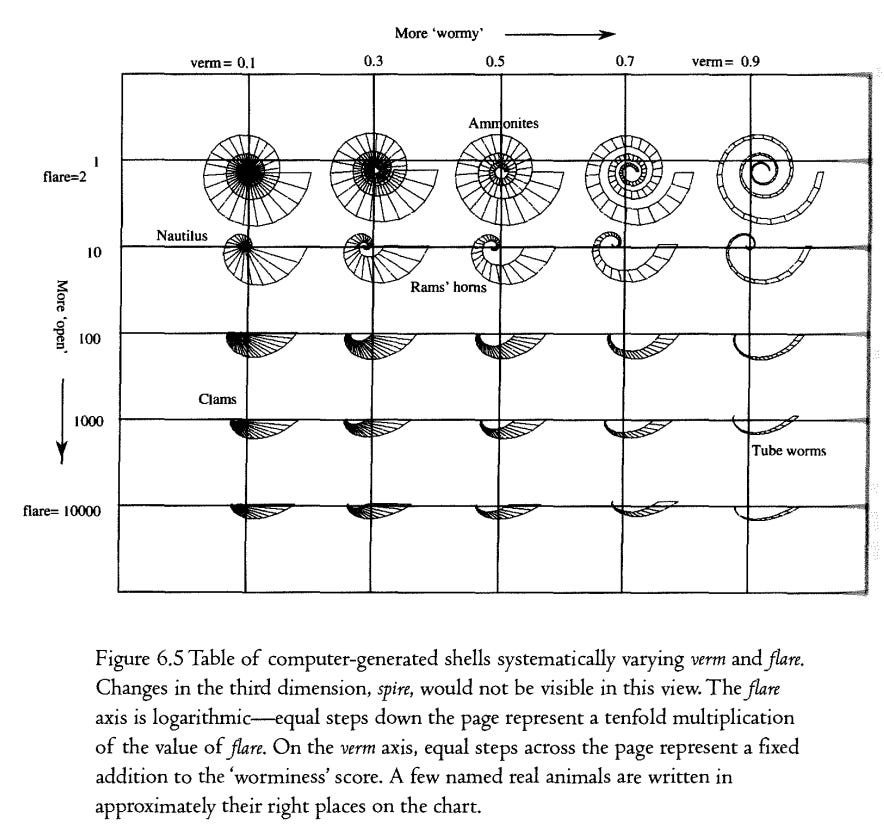
Raup described the spirals of shells using three numbers, which he called W, D and T. J hope it will not be thought too quaint if I rename them flare, verm and spire. It is easier to remember which is which than in the case of the mathematical letters. Flare is a measure of the expansion rate of the spiral. If the flare is 2, this means that, for every complete turn around the spiral, the spiral opens out to twice its previous size. This is true of Figure 6.2b. For every turn around Figure 6.2b, the width of the spiral doubles. Figure 6.2c, being a much more open shell, has a flare of 10. For each complete circuit around this spiral, the width would increase tenfold (although in practice the spital comes to an end before it has time to complete a whole circuit). Something like a cockle, which opens out so rapidly that you don't even think of it as coiling, has a flare value up in the thousands.

When describing flare I was careful not to say that it measures the rate of increase of the diameter of the tube. This is where the second number, verm, comes in. We need verm because the tube does not have to fill, snugly, the space made available by the expanding spiral. The shell can be ‘gappy’, like the one in Figure 6.3b. Verm gets its name from ‘vermiform’ which means ‘worm-shaped’. Figure 6.3a and Figure 6.3b have identical flare values (2) but Figure 6.3b has a higher verm score (0.7) than Figure 6.3a's 0.5. A verm of 0.7 means that the distance from the centre of the spiral to the inner margin of the tube is 70 per cent of the distance from the centre of the spiral to the outer margin of the tube. It doesn't matter which part of the tube you use to make the measurement, the verm score is the same (this doesn't logically have to be true but it seems often to be true of real shells and we shall assume it unless otherwise stated). You can easily see that a very high verm like 0.99 makes for a very thin, threadlike tube, because the inner margin of the tube is 99 per cent of the distance to the outer margin of the tube.

What verm value is needed to ensure snug fitting, as in Figure 6.3a? That depends on the flare. To be precise, the critical verm value for a snug fit is exactly the reciprocal of the flare value (that is, one divided by flare). The flare is 2 in both parts of Figure 6.3, so the critical verm for a snug fit is 0.5, and this is what Figure 6.3a has. Figure 6.3b has a verm which is higher than its ‘snug critical’ value, which is why the shell appears gappy. If we take a shell like Figure 6.2c with a flare value of 10, the snug critical verm score would be 0.1.

What if the verm value is smaller than the snug critical value? Could we imagine a tube so fat that it goes beyond snug fitting and actually encroaches inside the territory of the previous whorl—for example, a spiral like those in Figure 6.3 but with a verm value of, say, 0.4? There are two ways in which the clash can be resolved. One is simply to allow the tube to enclose earlier whorls of itself. Nautilus does this. It means that the shape of the cross-section of the available tube can no longer be a plain circle but has a ‘bite’ taken out of it. But this is no disaster because, as you'll remember, it was only an arbitrary decision to assume that the tube has a circular section in any case. Many molluscs live happily in a tube which is far from circular in section, and we shall come on to them. In some cases the best way to interpret the non-circular shape of the cross-section of the tube is as a means of accommodating previous whorls of the tube.

The other way to resolve the would-be encroachment of previous whorls of the tube is to move out of the plane. This brings us to the third of our shell signature numbers, spire. Think of the expanding spiral as moving sideways as it expands, making a conical shape like a top. The third shell signature number, spire, is the rate at which successive whorls of the spiral creep along the length of the cone. Nautilus happens to have a spire value of 0: all its successive windings are in one plane.

So, we have three shell signature numbers, flare, verm and _ spire (Figure 6.4). If we ignore one of these, say spire, we can plot a graph of the other two on a flat piece of paper. Every point on the graph has a unique combination of flare and verm values, and we can program the computer to draw, at that point, the shell that would be produced. Figure 6.5 shows twenty-five regularly spaced points on the graph. As you move from left to right across the graph, the computer shells become progressively more ‘wormy’ as verm increases, As you move from top to bottom and flare increases, the spitals become progressively more open until they don't look obviously spiral at all. In order to get a good spread as we go down, we make flare increase logarithmically. This means that each equal step down the page corresponds to multiplying by some number (in this case ten) rather than, as in a normal graph and as in the progression of verm-scores across the page, adding a number with each step. This is necessary in order to accommodate shells like cockles and clams, at the bottom left of the picture (which have flare values up in the thousands where small changes don’t make much difference) in the same graph as ammonites and snails (which typically have flare scores in low, single figures where small changes make a big difference). In various parts of the graph you can see shapes that resemble ammonites, Nautilus, clams, rams’ horns and tubeworms, and I’ve written labels in approximately the right places.

My computer program can draw shells in two views. Figure 6.5 shows one view, emphasizing the shape of the spiral itself. Figure 6.6 shows the other view, “X-ray’ cross-sections, giving an impression of the solid shape of the shells. Figure 6.7 is an actual X-ray photograph of real shells to explain the nature of this view. The four shells of Figure 6.6 are computer shells chosen, like the real shells of Figure 6A, to illustrate different values of flare, verm and spire.

Figure 6.8 is a graph, similar to Figure 6.5 except that the computer shells are shown in X-ray view, and the axes are flare and spire instead of flare and verm.

One could also, of course, plot verm versus spire, but I won't take the space to do this. Instead, I'll go straight to Raup’s famous cube (Figure 6.9). Because three numbers suffice to define a shell (leaving aside the question of cross-sectional shape of the tube) you can place each shell in its own unique spot in a three-dimensional box. The Museum of Possible Shells, unlike, say, the Museum of Possible Pelvis Bones, is a simple tower block. One dimension corresponds to each of the three shell signature numbers. Stand in the Museum of Possible Shells and walk, say, north, which we'll designate the verm dimension. As you make your way along the gallery, the shells that you pass steadily become more ‘wormy’, while keeping everything else constant. If at any point you turn left and walk west, the shells that you pass steadily increase their spire value, becoming more coneshaped, while keeping other things constant. Finally if, at any point, you stop moving either west/east or north/south and climb directly downwards instead—the flare dimension—you encounter shells with a steadily increasing rate of opening out. You can get from any shell to any other by burrowing through the cube at the appropriate angle, and you'll pass a continuous series of intermediate shells on the way. Figures 6.5 and 6.8 can be thought of as two outer faces of Raup’s cube. On two-dimensional paper we could print any slice, at any particular angle, through the cube.

Raup wrote the original computer program that is the inspiration for mine. In his published diagram, rather than attempt the impractical task of drawing all the shells in the cube, Raup sampled particular points. The pictures round the edge of Figure 6.9 represent the theoretical shells that you would find at the designated points of the space. Some of them look like actual shells that you might find on a beach. Others look like nothing on earth, but they still belong in the space of all computable shells. Raup shaded in on his picture those regions of the space where actual shells are to be found.

Ammonites, those once-ubiquitous Nautilus-relatives who seem to have come to the same sad end (whatever it was) as the dinosaurs, had coiled shells but, unlike snails, their coils were nearly always limited to one plane. Their spire value was zero. At least, this is true of typical ammonites. Pleasingly, however, a few of them, such as the Cretaceous genus Turrilites evolved a high spire value, thereby independently inventing the snail form. Such exceptional forms apart, the ammonites are housed along the eastern wall of the Museum of Shells (names like ‘east’ and ‘south’ are, of course, arbitrary labels for the diagram). The cabinets of typical ammonites don't occupy more than the southern half of the eastern wall, and only the top few storeys. Snails and their kind overlap with the Ammonite Corridor but they also spread far to the west (the spire dimension) and they penetrate a little further down towards the lower storeys of the tower block. But most of the lower storeys—where the flare rate is large and shells open out rapidly—belong to the two great groups of double-shelled creatures. Bivalve molluscs stretch a little to the west-—they have a slight twist on them like snails but their tube opens out so fast that they don’t look like snails. Brachiopods or ‘lamp-shells’, which, as we have seen, are not molluscs at all but superficially resemble bivalve molluscs, share with ammonites a ‘coil’ that is entirely in one plane. As with the molluscan bivalves, brachiopod tubes typically flare completely open before they have time to build up a ‘coil’ worthy of the name.

Any particular evolutionary history is a trajectory through the Museum of All Possible Shells and I have represented this by embedding my shell-drawing computer procedure in the larger, Blind Watchmaker artifictal-selection program. I simply removed the tree-growing embryology from the Blind Watchmaker program and dropped a shell-growing embryology into its place instead. The combined program is called Blind Snailmaker. Mutation is equivalent to small movements in the museum—remember that all shells are surrounded by their most similar neighbours. In the program, the three shell signature numbers are each represented by one gene locus whose numerical value can vary. So we have three classes of mutation, small changes in flare, small changes in verm and small changes in spire. These mutational changes can be positive or negative, within limits. The flare gene has a minimum value of I (smaller values would indicate a shrinking rather than a growth process) and no fixed maximum value. The verm gene's value is a proportion, varying from 0 to just below I (a verm of I would indicate a tube so thin and wormy as to be non-existent). Spire has no limits: negative values trivially indicate an upside-down shell. Following the original Blind Watchmaker program, Blind Snailmaker presents a parent shell in the middle of the computer screen, surrounded by a litter of asexual offspring—its randomly mutated near neighbours in the Museum of All Shells. The human selector clicks the mouse to choose one of the shells for breeding. It glides to the parental position in the centre, and the screen fills up with a litter of its offspring. The process recycles as long as the selector has patience. Slowly, you feel yourself creeping through the Museum of All Possible Shells. Sometimes you are walking amidst familiar shells, of the kind that you could pick up on any beach. At other times you stray outside the bounds of reality, into mathematical spaces where no real shells have ever existed.

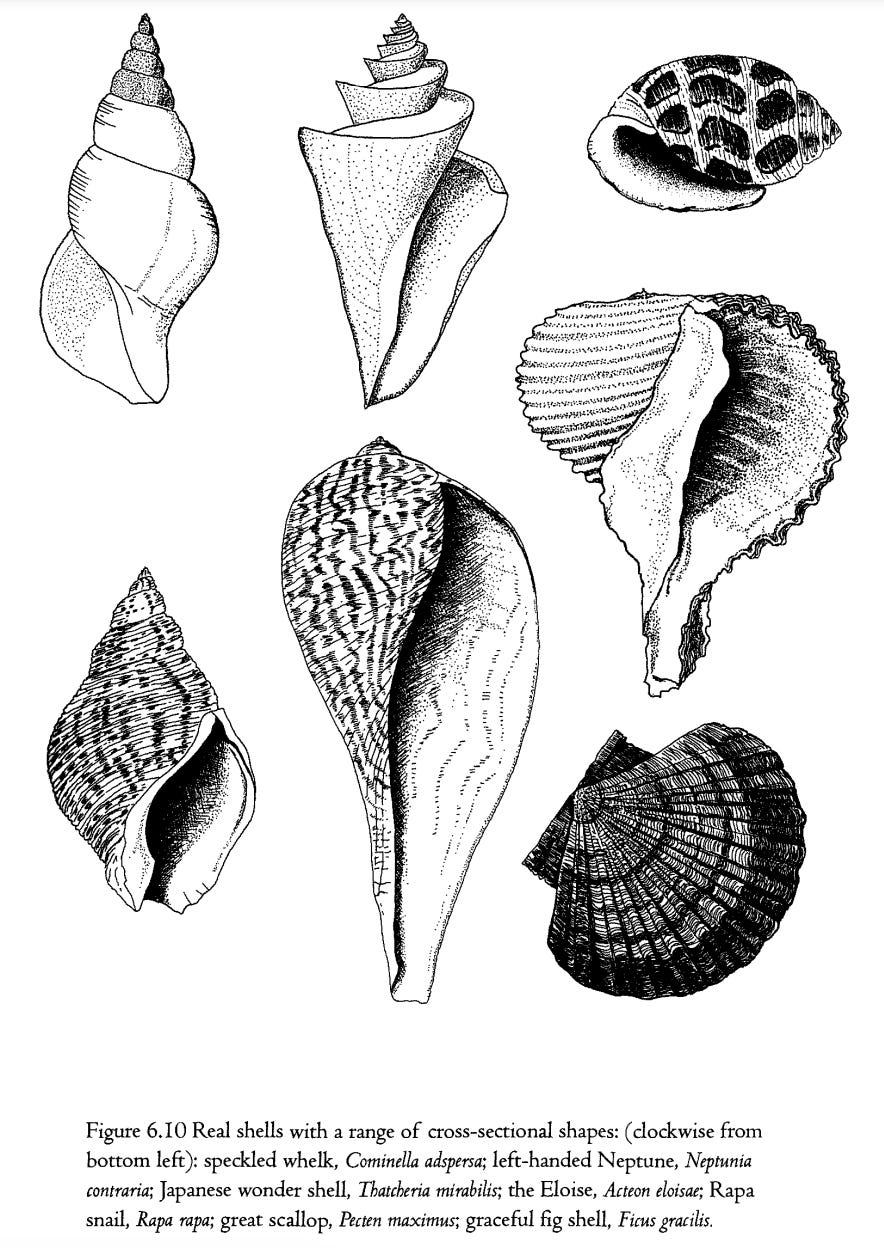
I earlier explained that, although the set of all possible shells can largely be described with only three numbers, this does include a simplifying assumption which is wrong: the assumption that the cross- sectional shape of the tube is always a circle. It seems to be generally true that, as the tube flares out, it remains the same shape, but it is by no means true that that shape is always a circle. It can be an oval and my computer model incorporates a fourth ‘gene’, called shape, whose value is the height of the oval tube divided by its width. A circle is the special case of a shape of I. Incorporation of this gene adds surprisingly to the power of the model to represent real shells. But it still is not enough. Many real shells have a variety of more complicated cross-sectional shapes which are neither circular nor oval, and which don't lend themselves to simple mathematical description. Figure 6.10 shows a range of shells which, as well as coming from different parts of the cubic museum, also have complicated, non-circular cross-sections of their basic tube.

My Blind Snailmaker program incorporates this extra variation by the rather crude expedient of providing a repertoire of predrawn cross-sectional outlines. Each of these outlines is then transformed (flattened vertically or horizontally) by the current (and mutable) value of the gene shape. The program then generates a tube of that transformed outline, sweeping it around and out just as if it were a circular tube. A better way to handle this problem—and one which J might attempt one day—would be to program the computer to simulate the actual growth process varying around the leading edge of the tube and thereby form ornate cross-sections. Nevertheless, for what it is worth, Figure 6.11 is a ‘zoo’ of “computer shells produced by the existing program, through artificial seJection using the human eye. They were bred for resemblance to known shells, some of them approximately similar to those of Figure 6.10, some of them similar to other shells that you might find on a beach or while diving.

The cross-sectional shape of the tube can be regarded as an additional dimension (or set of dimensions) in the Museum of All Shells. Setting that on one side and reverting to our simplifying assumption of a circular cross-section, one of the beauties of shells is that they are easy to fit into a Museum of All Possible Forms that we can actually draw in three dimensions. But this doesn’t mean that all parts of the theoretical museum are tenanted in real life. In real life, as we have seen, most of the volume of the museum tower block is empty. Raup shaded the lived-in regions (Figure 6.9), and they constitute much less than half the volume of the cube. Stretching far to the north and west, gallery after gallery houses hypothetical shells that could exist according to the mathematical model but which actually have never been seen on this planet. Why not? And why, since we are asking such questions, are the shells that have really existed confined to this particular cuboidal building in the first place?

What might a shell look like if it did not fit into the mathematical tower block? Figure 6.12a shows a computer-generated snail that doesn't. Instead of having a fixed spire value, its spire value changes as it grows older. More recent, wider, parts of the shell grow with a lower spire value than developmentally earlier, narrower, parts of the shell. This is why the whole shell has such an ‘unnaturally’, and presumably vulnerably, pointed top. This snail is hypothetical. It exists in the computer only. The computer ‘cone’ shell in Figure 6.12b also has an unnaturally pointed top. It too was drawn by the Blind Snailmaker program, but with the spire value programmed to decrease, rather than remain constant, as development proceeded.

The shells in Figure 6.13 are real, and I suspect that they too have a spire gradient, meaning that they begin life with a high spire value and gradually decrease it as they grow older. According to Raup, there were some real ammonites that changed their shell signature numbers as they grew older. You could say that as they grow older these odd shells move from one part of the museum to another and that they still stay within the museum. But it is also true to say that, since the juvenile body is included as part of the adult one, there is no one cabinet in the museum where the whole body can be housed. People could disagree over whether the animals in Figure 6.13 should be regarded as truly confined to the three dimensions of the box. Geerat Vermeij, one of today’s leading experts on the zoology of shelled animals, believes that a tendency to change signature numbers as the animals grow older may be the norm rather than the exception. He believes, in other words, that most molluscs shift their position in the mathematical museum, at least a little bit, as they grow up.

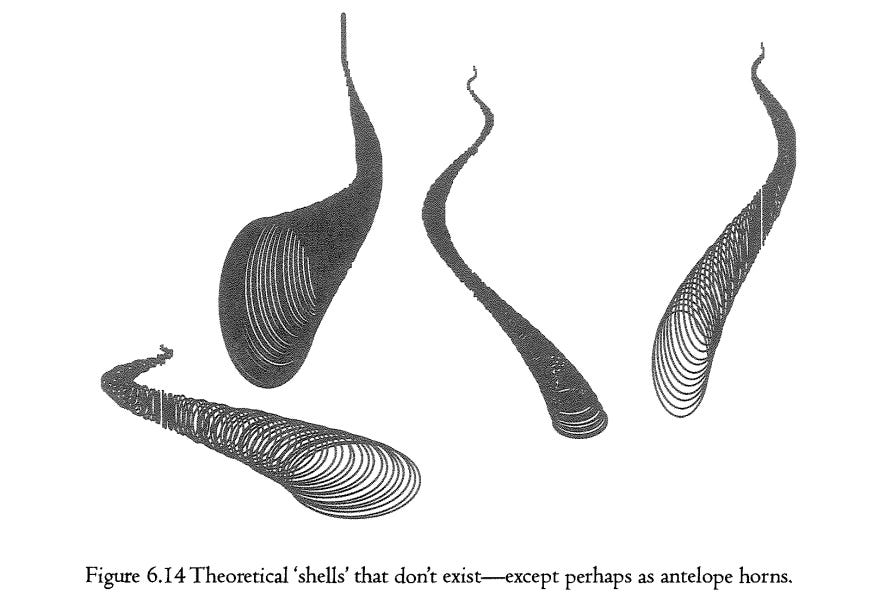
Let us turn to the opposite question of why large areas of the museum are empty of real shells. Figure 6.14 shows a sample of computer-generated shells from deep in the ‘no-go’ regions of the museum. Some of them might look fine on the head of an antelope or bison, but as mollusc shells they have never seen the light of day. With the question of why there are no shells like this, we come right back to the controversy with which we began. Is evolution limited by lack of available variation, or is it that natural selection doesn’t even ‘want’ to visit certain areas of the museum? Raup himself interpreted the empty areas—the unshaded zones of his cube—in selectionist terms. There is no selection pressure on shellfish to move into the areas represented by the gaps. Or, to put it another way, shells with those theoretically possible shapes would, in practice, have been bad shells in which to live: perhaps weak and easily crushed; or otherwise vulnerable, or uneconomical of shell material.

ther biologists think that the mutations that were needed to move into these areas of the museum were just never available. Another way of putting this view is to say that the tower block of conceivable shells that we have drawn is not, in fact, a true representation of the space of all possible shells. According to this view large areas of the tower block would not be possible even if they were desirable from a survival point of view. My own instinct favours Raup’s selectionist interpretation but I don’t want to pursue the matter for the moment because, in any case, I only introduced shells as an illustration of what we mean by mathematical spaces of possible animals.

I cannot leave the ‘no-go’ areas without briefly looking at some oddities that really do exist in the world. Spirula is a small, swimming cephalopod mollusc (the group that includes squids and ammonites) related to Nautilus. The opened-out shape of the shell betokens a high verm (larger than I/flare), and we have already met Spirula in this capacity in Figure 6.4. If it is suggested that high verm shells like this normally don't survive because they are structurally weak, Spirula fits the suggestion rather well. It doesn't live inside its shell but uses it as an internal flotation organ. Since the shell doesn’t serve for protection, nature allowed it to follow an evolutionary trajectory into what is normally a no-go region of the Museum of All Possible Shells. It is still firmly within the cube of the museum. This may be true of the West Indian tube shell drawn in Figure 6.15. which has taken up the way of life—and the shape—of a tube worm. Go to the bottom right of Figure 6.8 and you'll at least be in the general area of the museum where the West Indian tube shell is housed. On the other hand, close relatives of this creature (and also some extinct ammonites) have a much odder, less regular shape and they certainly cannot be housed in any one part of the museum.

Not only does our three-dimensional museum ignore the fact that tube cross-sections are not necessarily circles. It also ignores the rich patterns on the surface of shells: the tiger stripes and leopatd spots of Figure 6.10, the V-form calligraphy of Figure 6.4a and the whole repertoire of flutings and ridgings to be found sculpted and painted on other shells. Some of these patterns could be accommodated in our model by an instruction to the computer, as follows: as you sweep round and round, building up the expanding tube as a series of rings, make every nth ring thicker than the rest. Depending upon the value of n this rule could show itself as vertical stripes at a particular spacing on the surface of the shell. More complicated rules for the computer can generate more elaborate patterns. A German scientist called Hans Meinhardt has made a special study of such rules. Figure 6.16 shows the surface patterns on two teal shells, an olive shell and a volute, on the left. On the right are the strikingly similar patterns generated by computer rules implemented by Meinhardt’s computer program. You can see that his rules produce results akin to those that grow tree-like biomorphs, but he thinks of them in terms not of twigs growing but of waves of pigment-secreting and inhibiting activity sweeping over cells. The details are found in his book, The Algorithmic Beauty of Sea Shells, but I must leave this subject and return to my main theme of the Museum of All Shells.

I introduced the idea of the museum because of the singular fact that—setting aside the complications of tube cross-section, ornament and variable signatures—most known variants among shells can be approximated using a mere three numbers plugged into a drawing rule. To accommodate animal forms other than shells, we shall usually have to imagine a museum built in a larger number of dimensions than we can draw. Difficult as it is to visualize the myriad-dimensioned Museum of All Possible Animals, it is easy to keep in our heads the simple idea that animals are housed near those that they most closely resemble, and that it is possible to move in any direction, not just straight along corridors. An evolutionary history is a snaking trajectory through some part of the museum. Since evolution is going on independently in all parts of the richly diverse animal and plant kingdoms, we can think of thousands of trajectories, tunnelling in different directions through different regions of the multi-dimensional museum (notice how far we have come from the very different metaphor of Mount Improbable).

Now the controversy with which we began can be re-expressed as follows. Some biologists feel that as you walk the long corridors of the museum what you will find is smooth gradations in all directions. Large portions of the museum are never, as a matter of fact, visited by living flesh and bone but, according to this view, they would be visited if only natural selection ‘wanted’ to nose its way into those portions. A different set of biologists, with whom IJ am less in sympathy but who may be right, feel that large portions of the museum are forever barred to natural selection; that natural selection might batter eagerly on the doors of a particular corridor but never be admitted, because the necessary mutations simply cannot arise. Other parts of the museum, according to an imaginative variant of this view, far from being barred to natural selection, act like magnets or sinks, sucking animals towards them, almost regardless of natural selection’s best efforts. According to this view of life, the Museum of Possible Animal Forms is not an evenly laid-out mansion of long galleries and stately corridors with smoothly changing qualities, but a set of wellseparated magnets, each one bristling with iron filings. The iron filings represent animals, and the empty spaces between the magnets represent intermediate forms which might or might not survive if they came into existence, but couldn't exist in the first place. Another, and probably better, way to express this view is to say that our perception of what constitutes an ‘intermediate’ or a ‘neighbour’ in animal space is wrong. True neighbours are those forms which, as a matter of fact, can be reached in a single mutational step. These may or may not look, to our eyes, like neighbours.

I have an open mind about this controversy although I lean in one direction. On one point, though, J insist. This is that wherever in nature there is a sufficiently powerful illusion of good design for some purpose, natural selection is the only known mechanism that can account for it. I do not insist that natural selection has the keys to every corridor of the Museum of All Possible Animals, and I certainly don't think that all parts of the museum can be reached from all other parts. Natural selection is very probably not free to wander where it will. It may be that some of my colleagues are right, and natural selection’s freedom of access as it snakes, or even hops, around the museum is severely limited. But if an engineer looks at an animal or organ and sees that it is well designed to perform some task, then I will stand up and assert that natural selection is responsible for the goodness of apparent design. ‘Magnets’ or ‘attractors’ in Animal Space cannot, unaided by selection, achieve good functional design. But now, let me soften my position just a little by introducing the idea of ‘kaleidoscopic’ embryologies.